how to find the area of a rhombus

Rhombus Calculator

Rhombus Shapes

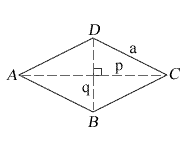
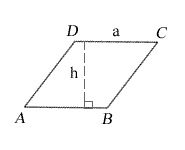
rhombus diamond shape labeled with angles, sides and diagonals rhombus shape labeled with angles, side and height
These 2 drawings refer to the same single rhombus.

a = side lengths
p = longer diagonal length
q = shorter diagonal length
h = height
A, B, C, D = corner angles
K = area
P = perimeter
π = pi = 3.1415926535898
√ = square root

Calculator Use

Calculate certain variables of a rhombus depending on the inputs provided. Calculations include side lengths, corner angles, diagonals, height, perimeter and area of a rhombus.

A rhombus is a quadrilateral with opposite sides parallel and all sides equal length. A rhombus whose angles are all right angles is called a square. A rhombus (or diamond) is a parallelogram with all 4 sides equal length.

Units: Note that units of length are shown for convenience. They do not affect the calculations. The units are in place to give an indication of the order of the calculated results such as ft, ft² or ft³. Any other base unit can be substituted.

Rhombus Formulas & Constraints

Corner Angles: A, B, C, D

A = C
B = D
A + B = 180° = π radians
for a rhombus that is not a square,
- 0 < A< 90° (0 < A < π/2)
- 90° < B < 180° (π/2 < B < π)

Area: K

with A and B in radians,

K = ah = a² sin(A) = a² sin(B) = pq/2

Height: h

h = h_a = h_b
h = a sin(A) = a sin(B)

Diagonals: p, q

p = a √( 2 + 2 cos(A) ) = a √( 2 - 2 cos(B) )
q = a √( 2 - 2 cos(A) ) = a √( 2 + 2 cos(B) )
p² + q² = 4a²

Perimeter: P

P = 4a

Rhombus Calculations:

The following formulas, based on those above, are used within this calculator for the selected calculation choices.

Calculate B, C, D | Given A
Given angle A calculate angles B, C and D
- B = 180° - A
- C = A
- D = B
Calculate A, C, D | Given B
Given angle B calculate angles A, C and D
- A = 180° - B
- C = A
- D = B
Calculate a | Given P
Given the perimeter calculate side a
- a = P / 4
Calculate P | Given a
Given side length a calculate the perimeter
- P = 4a
Calculate B, p, q, h, P, K | Given a, A
Given side length a and angle A calculate the diagonals, perimeter, height, area and angles B, C and D
- p = √( 2a² + 2a² cos(A) )
- q = √( 2a² - 2a² cos(A) )
- P = 4a
- h = a sin(A)
- K = ah
- B = 180° - A
- C = A
- D = B
Calculate A, B, q, h, P, K | Given a, p
Given side length a and diagonal p calculate diagonal q, perimeter, height, area and angles A, B, C and D
- A = arccos( 1 - (p² / 2a²) )
- q = √( 2a² - 2a² cos(A) )
- h = a sin(A)
- P = 4a
- K = a² sin(A)
- B = 180° - A
- C = A
- D = B
Calculate A, B, p, h, P, K | Given a, q
Given side length and diagonal q calculate diagonal p, perimeter, height, area and angles A, B, C and D
- A = arccos( 1 + (q² / 2a²) )
- p = √( 2a² + 2a² cos(A) )
- h = a sin(A)
- P = 4a
- K = a² sin(A)
- B = 180° - A
- C = A
- D = B
Calculate A, B, p, q, P, K | Given a, h
Given side length and height calculate the diagonals, perimeter, area and angles A, B, C and D
- A = arcsin(h/a)
- p = √( 2a² + 2a² cos(A) )
- q = √( 2a² - 2a² cos(A) )
- P = 4a
- K = a² sin(A)
- B = 180° - A
- C = A
- D = B
Calculate A, B, p, q, h, P | Given a, K
Given side length and area calculate the diagonals, perimeter, height and angles A, B, C and D
- A = arcsin(K/a²)
- p = √( 2a² + 2a² cos(A) )
- q = √( 2a² - 2a² cos(A) )
- h = a sin(A)
- P = 4a
- B = 180° - A
- C = A
- D = B
Calculate a, A, B, p, q, P | Given K, h
Given area and height calculate side length, diagonals, perimeter and angles A, B, C and D
- a = K / h
- P = 4a
- A = arcsin(K/a²)
- p = √( 2a² + 2a² cos(A) )
- q = √( 2a² - 2a² cos(A) )
- B = 180° - A
- C = A
- D = B
Calculate a, A, B, q, h, P | Given K, p
Given diagonal p and area calculate the perimeter, height, side length, diagonal q and angles A, B, C and D
- q = 2K / p
- a = √(p² + q²) / 2
- P = 4a
- A = arccos( 1 - (p² / 2a²) )
- h = a sin(A)
- B = 180° - A
- C = A
- D = B
Calculate a, A, B, p, h, P | Given K, q
Given diagonal q and area calculate the perimeter, height, side length, diagonal p and angles A, B, C and D
- p = 2K / q
- a = √(p² + q²) / 2
- P = 4a
- A = arccos( 1 + (q² / 2a²) )
- h = a sin(A)
- B = 180° - A
- C = A
- D = B
Calculate a, B, p, q, P, K | Given A, h
Given angle A and height calculate side a, angles B, C and D, diagonals, perimeter and area
- a = h / sin(A)
- P = 4a
- p = √( 2a² + 2a² cos(A) )
- q = √( 2a² - 2a² cos(A) )
- K = a² sin(A)
- B = 180° - A
- C = A
- D = B
Calculate a, A, B, h, P, K | Given p, q
Given diagonal p and diagonal q calculate the side length, angles A, B, C and D, height, perimeter, and area
- a = √(p² + q²) / 2
- P = 4a
- K = (p * q) / 2
- A = arcsin( K / a²)
- B = 180° - A
- C = A
- D = B
- h = a sin(A)

References

Zwillinger, Daniel (Editor-in-Chief). CRC Standard Mathematical Tables and Formulae, 31st Edition New York, NY: CRC Press, p. 323, 2003.

Weisstein, Eric W. "Rhombus." From MathWorld--A Wolfram Web Resource. Rhombus.

Follow CalculatorSoup: